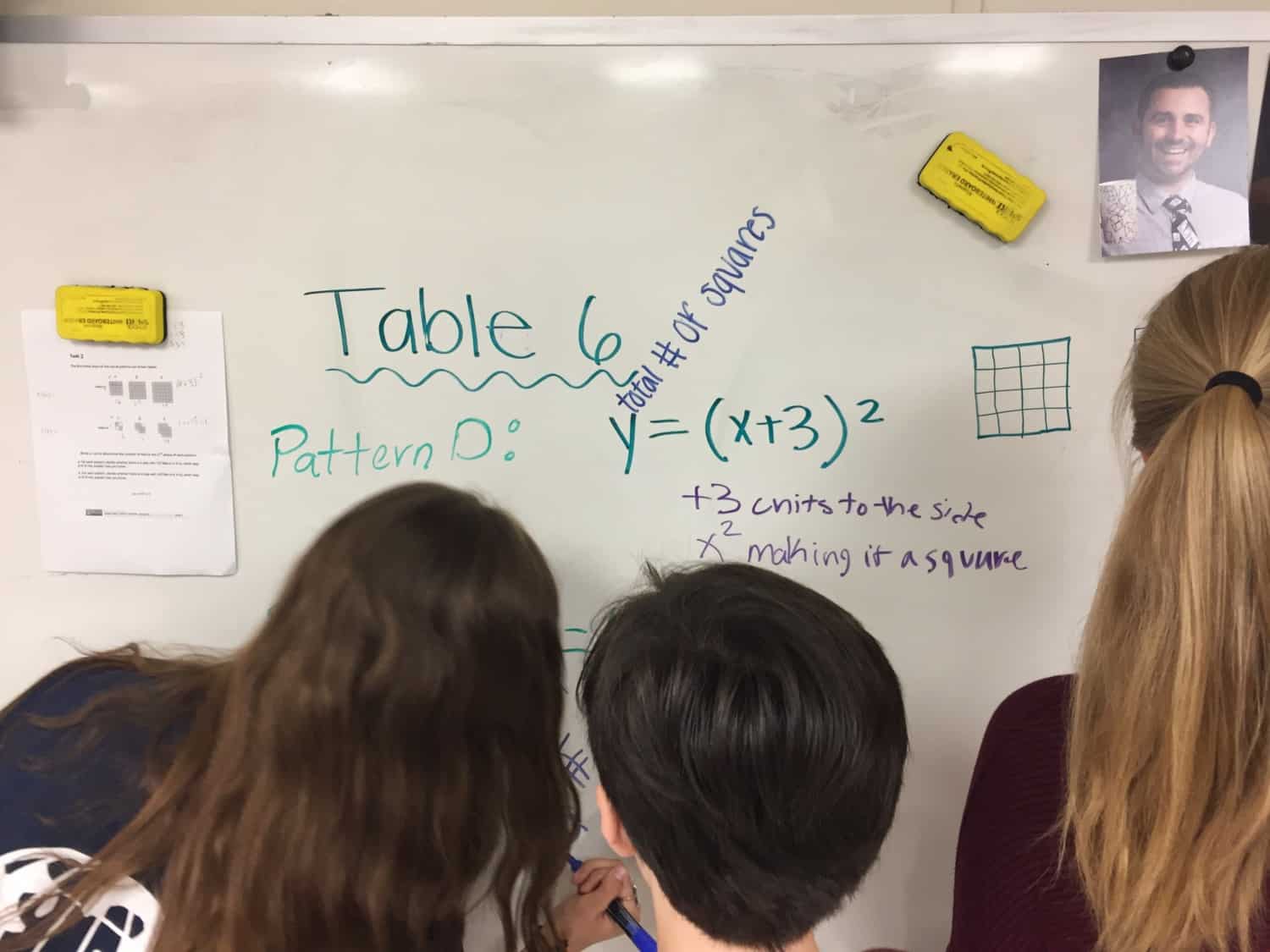And why the coherence of an integrated curriculum across grade levels is important.
“We did this last year,” one of my 9th grade students quickly announces as I finish drawing a right triangle on the whiteboard.
I quickly respond to this student, “Cool! Well, what do you know about this?” And the student will begin to recite any and every thing they know about right triangles, which almost always begins with Pythagorean theorem.
To which I respond, “Alright, let’s go a little deeper…”

We start out with just the shape of a triangle and its properties, expanding that understanding to develop new ideas like triangle inequality and special right triangles. We then link what we already know about lines and their slopes, combining with properties of similar right triangles, to develop a set of ratios (which are just the basic trigonometric ratios).
Over the course of two weeks, we begin to model these ratios as they relate to other mathematical principles. We investigate the mathematics behind finding a particular length without being able to actually measure it (a skill used in surveying land plots and constructing buildings). All the while students are incorporating this new information into what they already know about the right triangle I drew on the board the first day.
This process is called assimilation, and is the foundation of Jean Piaget’s adaptation process for cognitive development, which is all a part of the complex task of learning. It is the idea that we learn by incorporating new knowledge into their our pre-existing understanding of a topic.
This is the very foundation of integrated math:
Building from students’ prior knowledge, connecting topics that used to seem unrelated, and applying these skills to solve new problems.
This is not only an eye-opening way of exploring the world of mathematics, but a foundational skill of learning, not just utilized in a math class.
There has been much debate over the math standards in our state, and around the country. The process has been grueling. However, it is important to differentiate the standards from the curriculum. The standards are our destination, while integrated math is the vehicle we choose to get there.
Integrated math is not a new concept. The state of New York began teaching integrated math in the 1970s. The top performing countries, who have continually outscored the U.S. in mathematics, teach an integrated curriculum. But what does it actually mean to be integrated?
To understand how this curriculum benefits our students, we can’t solely look at a single grade’s connection of geometry and algebra, but we have to span across grade-levels to see the process of assimilation in learning fundamental concepts of mathematics.
Below is an example of how basic arithmetic properties can relate to shapes and their properties spanning from elementary to high school Algebra in an integrated approach to mathematics.
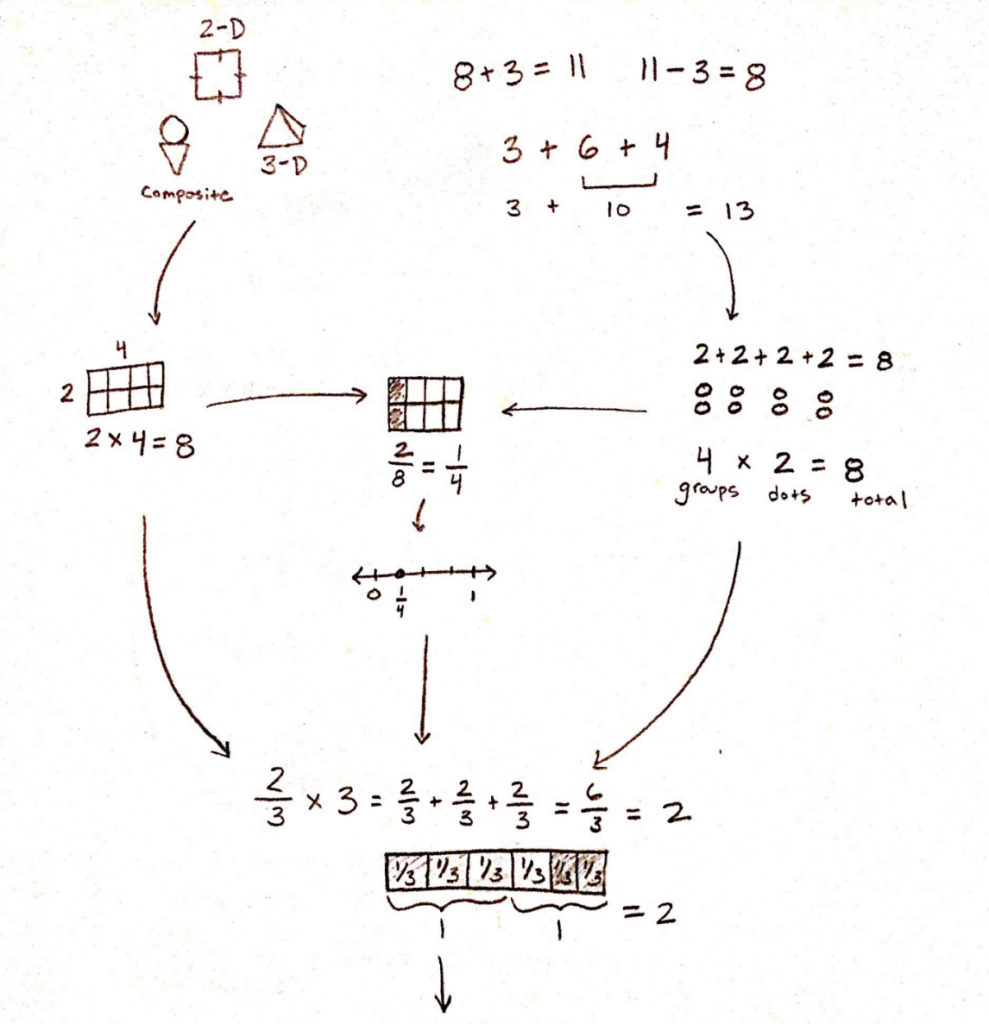
In 1st grade, students solidify their understanding of basic shapes and their properties (1.G.A.2), while simultaneously learning how to build their number sense using addition and subtraction (1.OA.B.3). Using shapes’ perimeters, students practice fluency with these basic algebraic operations.
In the 3rd grade, students explore the distributive property to define the operations of multiplication and division as repeated addition and subtraction. They use shapes’ areas to explain and practice these new operations (3.MD.C.5).
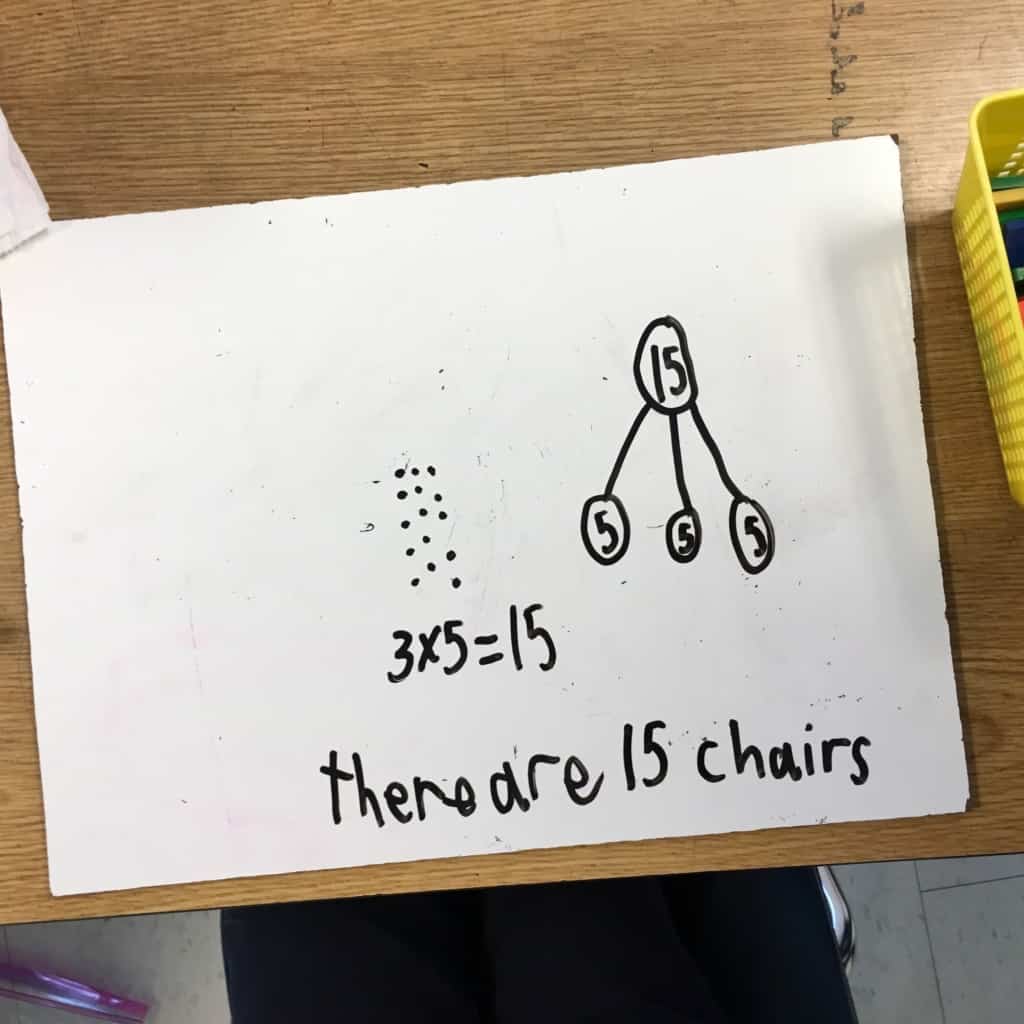

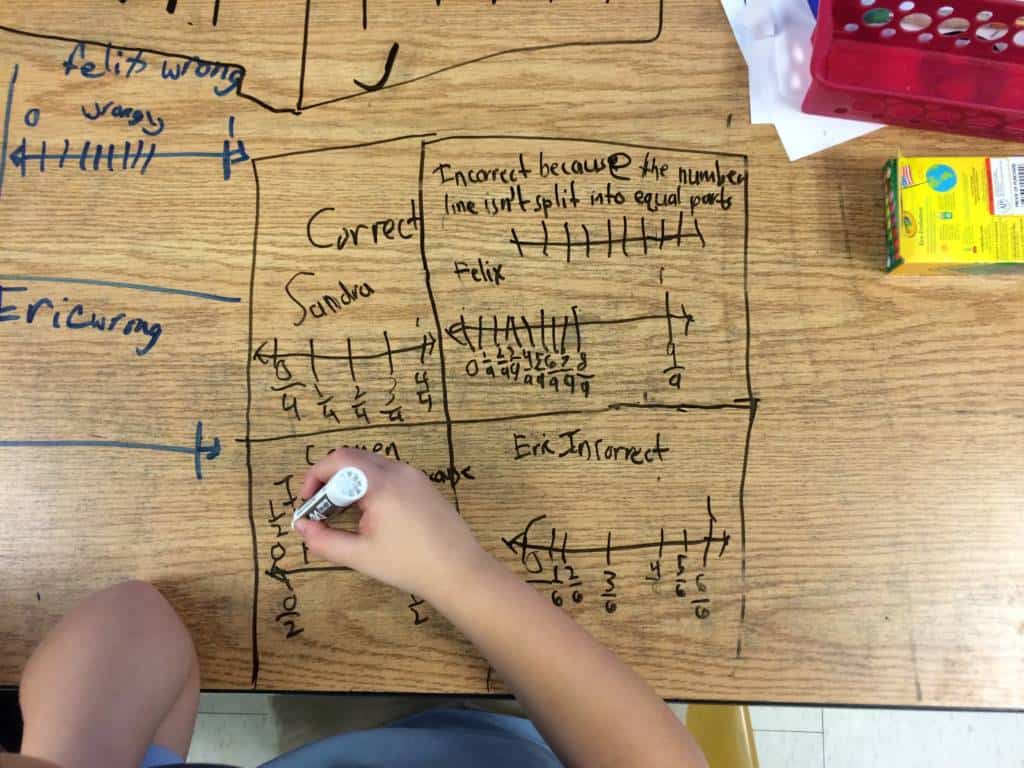
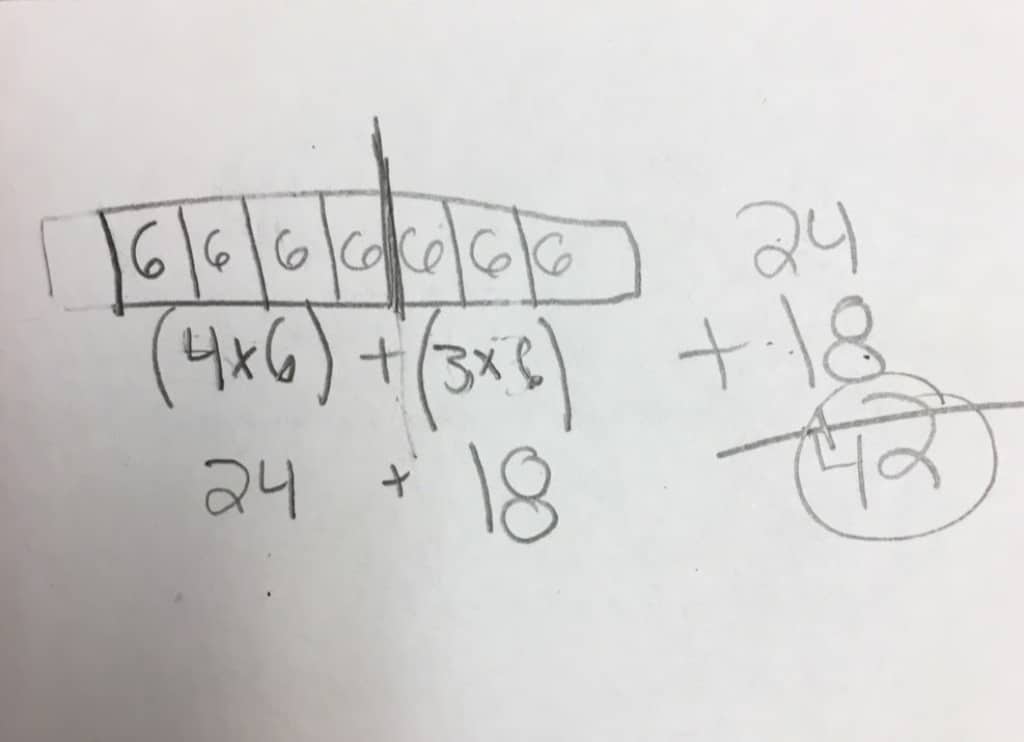
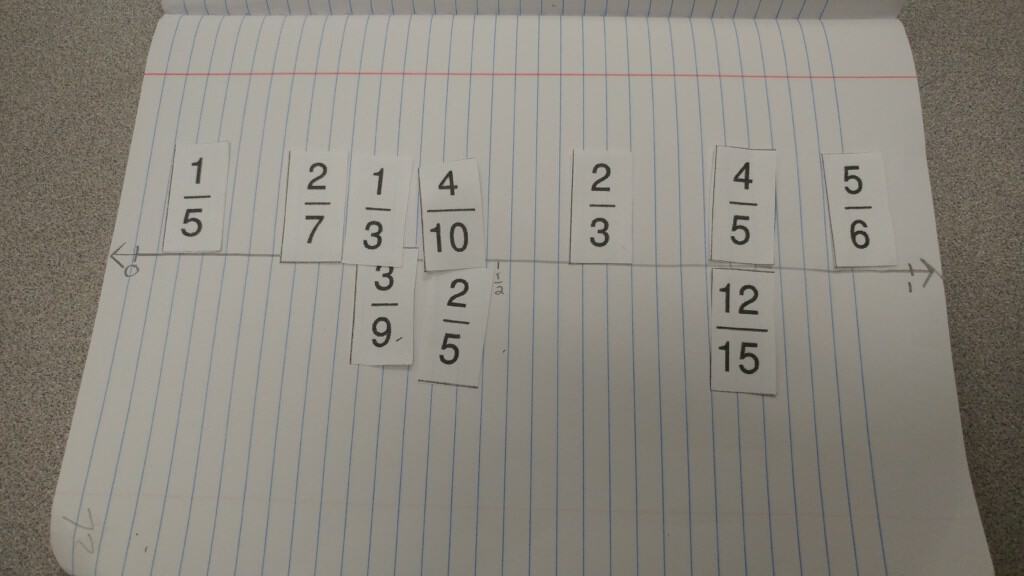
Using division, they discover fractions and describe using area models and number lines (a skill most useful in reading statistical analyses later on).
In the 5th grade, students use area models to understand operations with fractions and whole numbers. Drawing from their previous understanding of the operations as repeated addition/subtraction (5.NF.B.4).
All the while students are being asked to reason algebraically for unknown quantities using the new operations they are learning. For example, a rectangle with the area 15 square units and a width of 3 units has to have a length of 5 units. This directly translates to the work of the middle grades in solving equations with unknown quantities (i.e. solve for x).
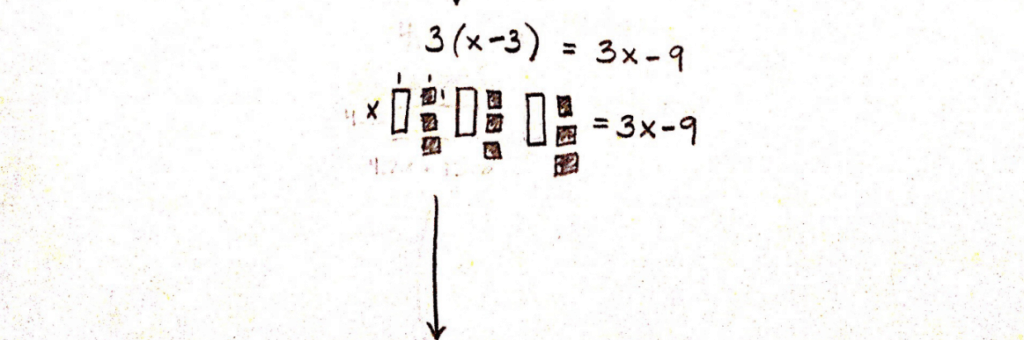
In 6th grade, students begin utilizing the dimensions of their shapes to represent various, unknown quantities to illustrate algebraic properties (6.EE.A.3). In this example, their previous understanding of the distributive property is being used to craft a visual algebraic model.
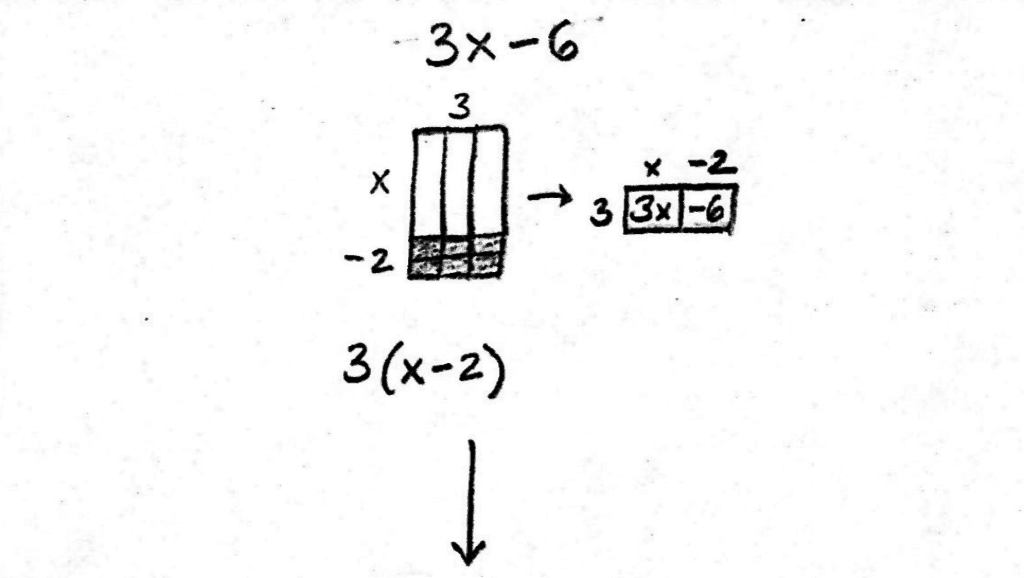
In 7th grade, students formalize their area models as a mean to demonstrate how to reverse the distributive property, dividing out a common factor from a linear expression to rewrite the expression into an equivalent form (7.EE.A.1). This is the beginning of a skill called factoring, used quite frequently (and often incorrectly by students) in high school mathematics to solve algebraic equations.
Once comfortable, students move from a detailed area model to a more generic area model writing the dimensions of the rectangles as the terms in the expression (right side of drawing).
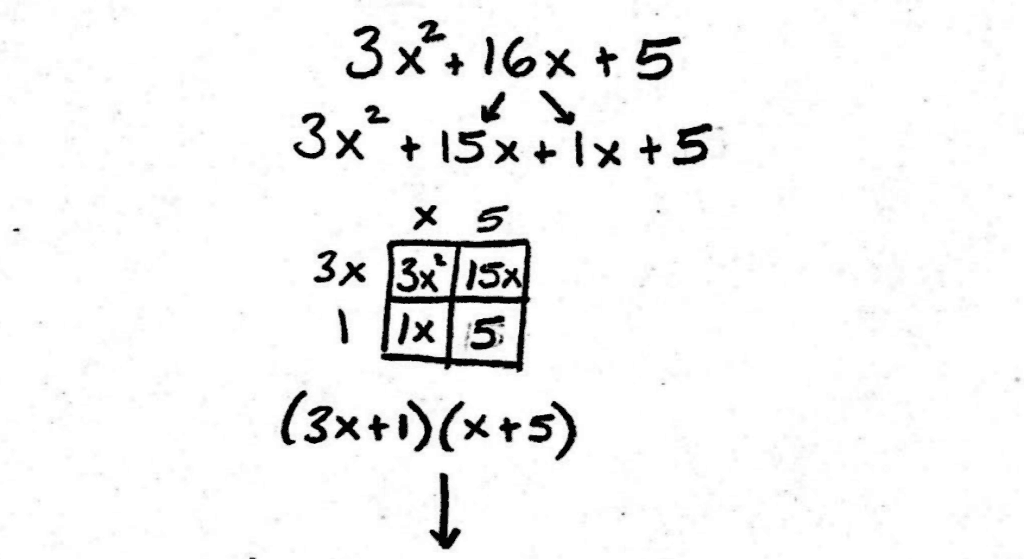
In 9th-10th grade, students begin using their newly learned skill of factoring to simplify more complex expressions (quadratics), expanding their area models to accommodate for more terms (HSA.SSE.A.2).
During this time, students are also using these expressions to build functions, and identify the various parts of their graphs. They begin applying these functions to real-world examples such as maximizing profit if minimizing costs in business.


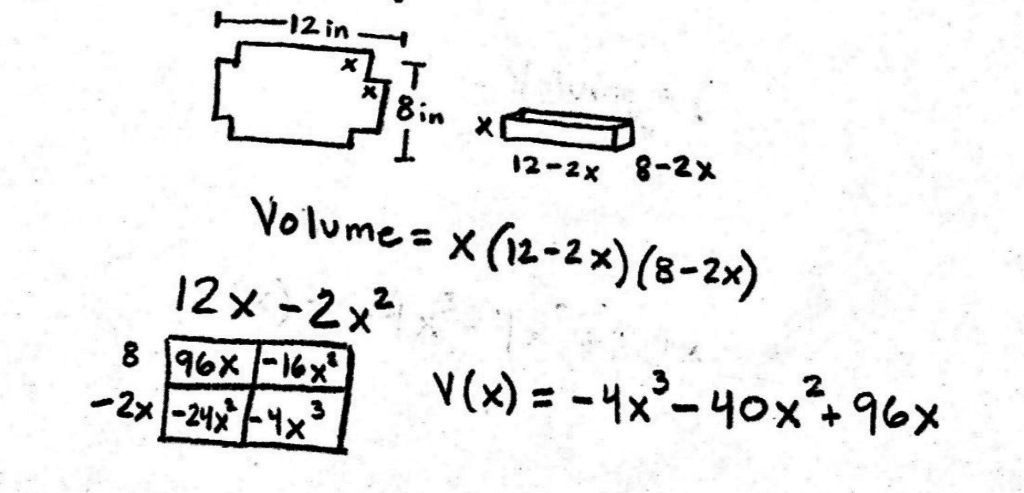
Then, in the 10th-11th grade, students extend their applications to include another term, creating a cubic expression. In this example, they have written the volume of a prism with unknown height from finite dimensions. From here, students could identify the maximum volume based on the material given, a skill valued in product design.
Further, students would be able to take this understanding of functions as they relate to area of shapes to a higher level of math, primarily Calculus.
If you made it all the way through that example, good job. If you got lost in the complexity (somewhere in middle school, no doubt), that’s okay because math is complex. A true understanding goes beyond an elementary understanding, which is what we are trying to demonstrate to students. Notice how this progression builds from the previous grade level’s work, expanding the applications. Students start building their algebraic understanding all the way back in first grade with their shapes and numbers. The very foundation of this approach is using kid’s natural learning process to grow their understanding.
If done correctly, an integrated approach not only demonstrates major connections in mathematics, but showcases a strong pedagogical understanding of how it should be taught — a method our current integrated curriculum has attempted to push into classrooms across our state. Good math teachers have been doing this for decades.
Teaching math should not be taught as separate files of information, stored away and readily accessed when a specific problem arises (that’s why we have computers), but as a toolbox of various strategies used to solve problems student may or may not encounter. It is through this integrated lens our states’ students can assimilate new ideas and topics and begin to truly understand math.
Recommended reading